
The digital display contains numerous magnetic components inside, which account for a significant proportion of the product cost. We can easily find various inductors, magnetic beads, transformers, etc. when searching for a product. However, perhaps due to the complex and variable parameters in magnetism, or perhaps because magnetic components appear too simple, most engineers tend to overlook them in product design. We know that in the design of switching power supplies, in order to achieve higher conversion efficiency, designers need to fully master the design techniques of transformer windings, air gaps, PFC inductors and other parameters. When designing EMI filters, we often focus on the inductance and impedance parameters of magnetic components, while neglecting many key parameters. Changhui Instrument will provide readers with a series of articles on the application of magnetic beads in digital displays to further understand the various characteristics of magnetic components, hoping to help readers select magnetic components more accurately in practical projects and analyze the causes of problems more quickly.
Magnetic beads are a type of magnetic component, which can be divided into core magnetic beads and patch magnetic beads. In my personal opinion, core magnetic beads are closer to inductors and are relatively rare in practical applications, especially in the current trend of product miniaturization, where surface mount magnetic beads have more advantages. Changhui Instrument focuses on the use of surface mount magnetic beads for instrument production in this article, hoping to be helpful to readers.
01
Ferrite Bead
Analog and digital ICs with different frequency and power characteristics in CB are typically powered by different power supply networks. This helps prevent fast digital switching noise from coupling to sensitive analog power networks, reducing converter performance, but independent power supply increases system level complexity and manufacturing costs. Ferrite magnetic beads are usually chosen for appropriate high-frequency isolation of power networks. Ferrite magnetic beads are passive devices that can filter high-frequency noise over a wide frequency range. It has resistance characteristics within the target frequency range and dissipates noise energy in the form of heat. In general, ferrite magnetic beads are mainly used in PDN power networks. Capacitors with appropriate capacitance values are usually connected to ground on both sides of the beads to form a filtering network and reduce the switching noise of the PDN power network. The equivalent circuit model of ferrite magnetic beads is a circuit composed of resistors, inductors, and capacitors. As shown in the following figure. RDC corresponds to the DC resistance of magnetic beads. CPAR, LBEAD, and RAC respectively represent parasitic capacitance, magnetic bead inductance, and AC resistance related to magnetic beads (AC core loss).
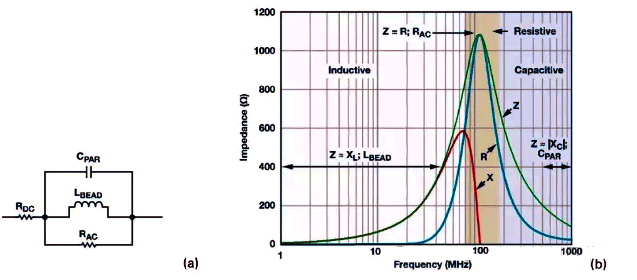
Figure 1 (a) Simplified circuit model of ferrite magnetic beads; Figure 1 (b) ZRX curve of ferrite magnetic beads measured using TycoElectronics BMB2A1000LN2
Jefferson Eco provided the results of four parameters in his article, and the calculation process is also very simple, which will not be repeated here. The specific value is RDC=300 𝑚𝛺, CPAR=1.678𝑝𝐹,LBEAD=1.208𝑢𝐻,RAC=1.082𝑘𝛺。 From the calculation results, the equivalent model of magnetic beads is an LCR parallel resonant circuit, and the contribution of RDC is ignored. The CST was used to establish the magnetic bead model, and the impedance parameters obtained are shown below. It can be seen that the overall results are consistent.
RAC is the most important parameter among the four parameters that make up magnetic beads. It is precisely because of the existence of RAC that magnetic beads are called magnetic beads. Otherwise, the model formed can only be called resistance. It is also because of the existence of RAC that the impedance curve shown in the following figure is formed. We all know the formula for calculating the resonant frequency of LC. If you calculate the resonant frequency of a resonant circuit composed of CPAR and LBEAD, you will find that its resonant frequency happens to be the highest point of the impedance curve. When the RLC parallel circuit resonates, the circuit admittance Y (j ω)=G=1/R, which means the impedance value corresponding to the resonance point is the value of RAC.
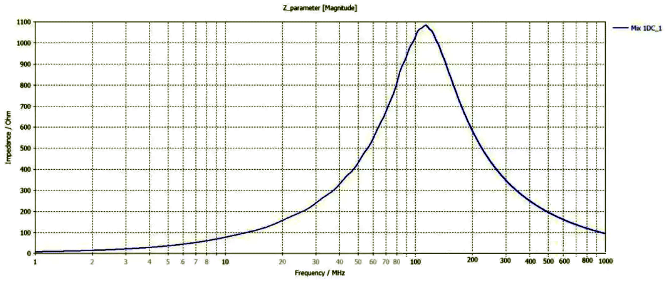
Figure 2: Impedance curve of magnetic beads calculated using CST
When the circuit operates similarly to a current source (we know that the characteristics of common mode noise are similar to current sources), the voltage on the RLC (i.e. magnetic bead) circuit is 𝑈=𝑅𝐴𝐶𝐼. At this point, the addition of magnetic beads will cause an increase in circuit noise. Similarly, because Q=𝜔𝐿𝑅=𝑅𝜔𝐶=𝑅 in the RLC parallel resonant circuit, the quality factor Q is directly related to 𝑅𝐴𝐶. In extreme cases, the addition of magnetic beads causes noise in the circuit, but rather the value of 𝑅𝐴𝐶 in the magnetic beads causes noise to rise in the circuit.
The actual magnetic beads are composed of multiple layers of ferrite medium and spiral electrodes inside. The conductivity of the ferrite medium material is about 10E-2 level, and the magnetic permeability is about 100. The conductivity of the medium and the size of the internal electrode jointly determine the values of 𝑅𝐴𝐶, 𝐶𝑃𝐴𝑅, and R 𝐷𝐶, while the magnetic permeability and the size of the internal electrode jointly determine the value of 𝐿𝐵𝐸𝐴𝐷. The magnetic bead on the PCB shown in the figure has an outer dimension of 4 × 4.6 × 1.85mm and a total of 4 turns of internal electrodes.
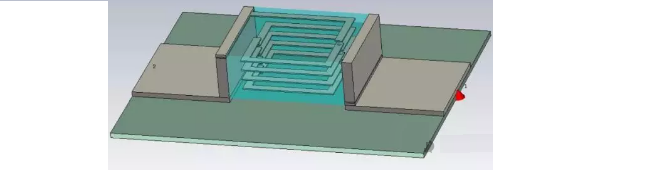
Figure 3 Internal structure of magnetic beads
From the results, it can be seen that the 𝐿𝐵𝐸𝐴𝐷 sensitivity of the magnetic bead is about 3.2uH, 𝐶𝑃𝐴𝑅 is about 3.6pF, and 𝑅𝐴𝐶 is about 1207 Ω.
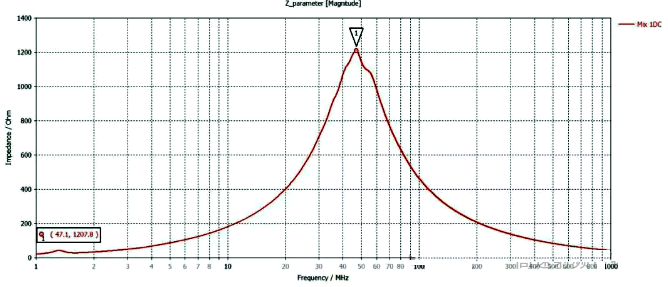
Figure 4 Impedance curve of magnetic bead model
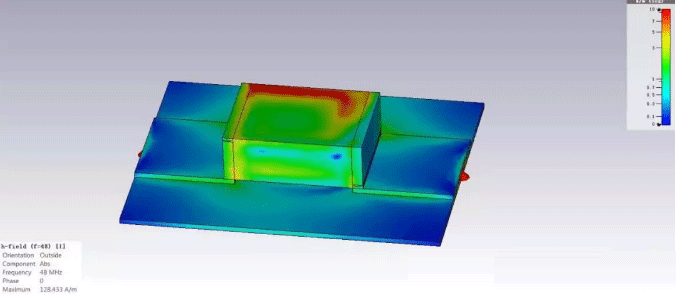
Due to the fact that the inner electrode of the magnetic bead is entirely wrapped in ferrite material, the magnetic bead itself has complete magnetic shielding, and the leakage of its external magnetic field is relatively small. Therefore, when conducting layout, there is no need to consider whether there are sensitive circuits around the magnetic beads, nor is there a need to deliberately excavate the layers below the magnetic beads.
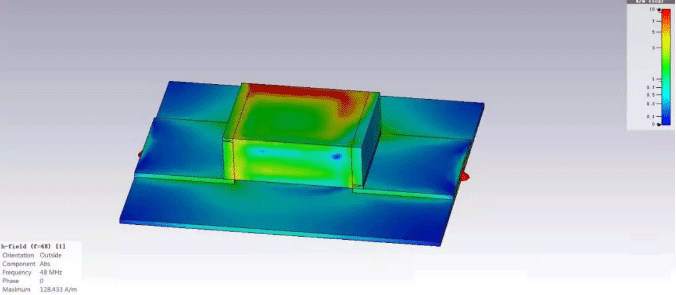
Figure 5 Magnetic field distribution of magnetic beads at the highest impedance frequency
02
Insertion loss of magnetic beads
In filter circuit design, insertion loss is the parameter that best reflects the characteristics of the filter circuit. When considering device selection in product improvement, we first look at the insertion loss characteristics of the device. Insertion loss can comprehensively reflect the ability of a circuit system to consume electromagnetic energy, which can be reflected back to the source end or converted into another type of energy through the device's own heating. However, the insertion loss parameter does not reflect the damping characteristics of the circuit system, which is also the most troublesome thing for most designers. Often, devices with correct parameters are applied in circuits, but the result is similar to what is introduced in the following sections, where the circuit noise increases instead of decreasing.
The following figure shows the testing system of Changhui Instrument, which uses a network analyzer and a specially designed fixture to test the S-parameters of magnetic beads and other devices. When using a 600R magnetic bead for testing, the results are shown in the figure.

Figure 6 Testing magnetic bead insertion loss using a network analyzer
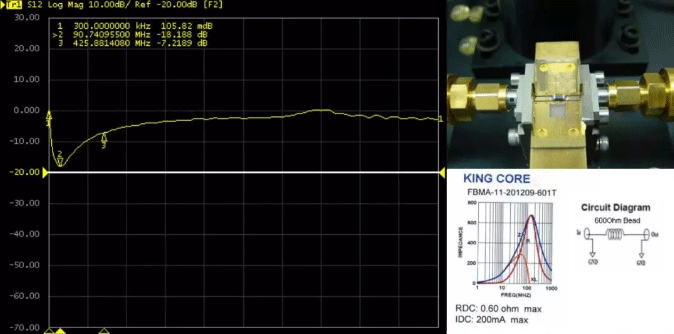
Figure 7 Insertion loss curve of magnetic beads
Because the impedance curve provided is not clear enough, here we approximately estimate 𝐿𝐵𝐸𝐴𝐷=1.59 𝑢𝐻, 𝐶𝑃𝐴𝑅=0.7𝑝𝐹,R𝐷𝐶=600𝑚𝛺,𝑅𝐴𝐶=680𝛺, The insertion loss curve calculated using this parameter is shown in the following figure. It can be seen that the calculated results have lower high-frequency insertion loss compared to the test. We assume that the testing equipment has been accurately calibrated, so the difference in the test results is due to the inaccurate impedance parameter curve of the product! According to the test, the lowest point of insertion loss is 90.74MHz and the insertion loss is 18.188dB. The parameters in the test system are written into the software, and after recalculation, the 𝐿𝐵𝐸𝐴𝐷 value of the magnetic bead is 1.59 𝑢𝐻, 𝐶𝑃𝐴𝑅=2.1𝑝𝐹,R𝐷𝐶=600𝑚𝛺,𝑅𝐴𝐶=715𝛺。 The distribution of the corrected insertion loss curve and impedance curve is shown in the following figure. We can see from the revised insertion loss curve that the insertion loss parameter at the Mark point is almost identical to the actual test.
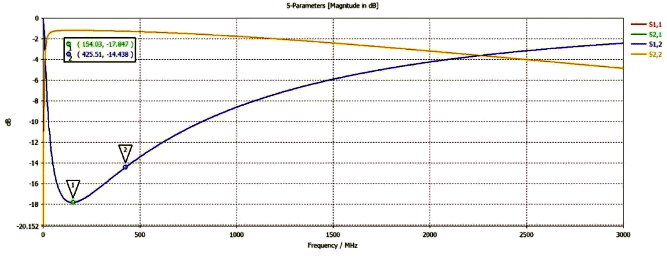
Figure 8: Insertion loss curve calculated based on product impedance curve
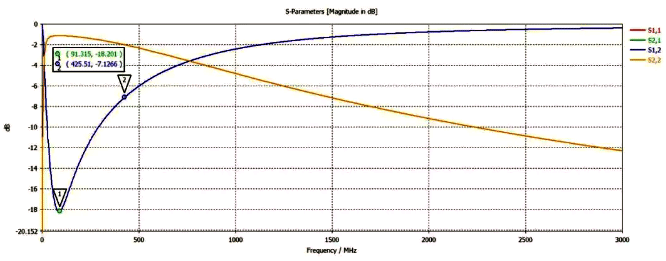
Figure 9 Revised Insertion Loss Curve
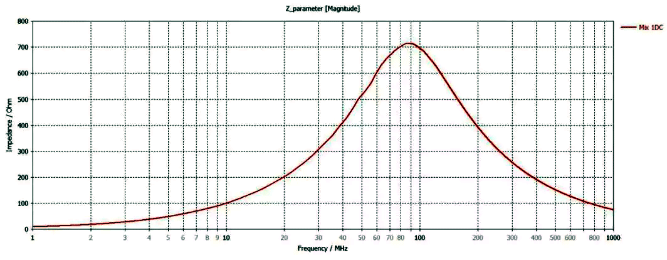
Figure 10: Revised Impedance Curve
Compared to inductors, the insertion loss characteristics of magnetic beads are relatively small. By using LC filtering alone in the circuit, a larger insertion loss value can be achieved, and even an insertion loss of 80dB can be achieved in actual testing. However, when using LC filtering alone, the insertion loss value will rapidly decrease when the frequency is higher than the LC resonance frequency, which we do not want to see. At this time, magnetic beads can be used to improve the high-frequency characteristics.
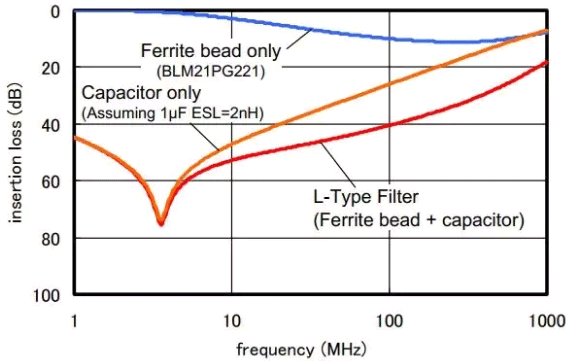
Figure 11 Insertion loss characteristics of ferrite beads used in L-shaped filtering circuit (calculated values)
03
Magnetic beads in the power supply
There are examples in Murata's information of using ferrite magnetic beads for noise suppression and improvement. As shown in the figure below, it can be seen that magnetic beads have a significant isolation effect on IC noise.
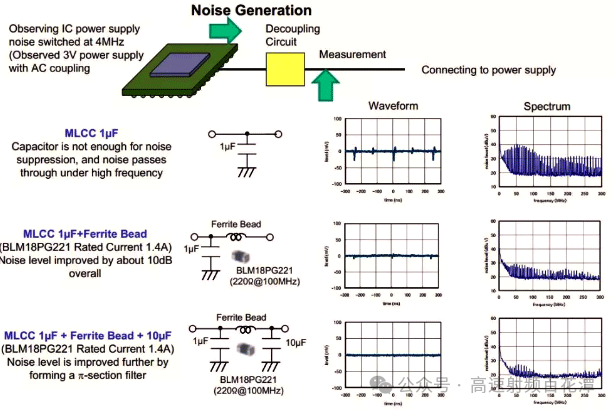
Next, we will use ANSYS Simplorer to build a Buck circuit with an input of 10V, an output of 3.5V, a switching frequency of 200kHz, and a duty cycle of 50%. We need to examine the waveforms of each component and the conduction noise of the switching transistor at the input end.
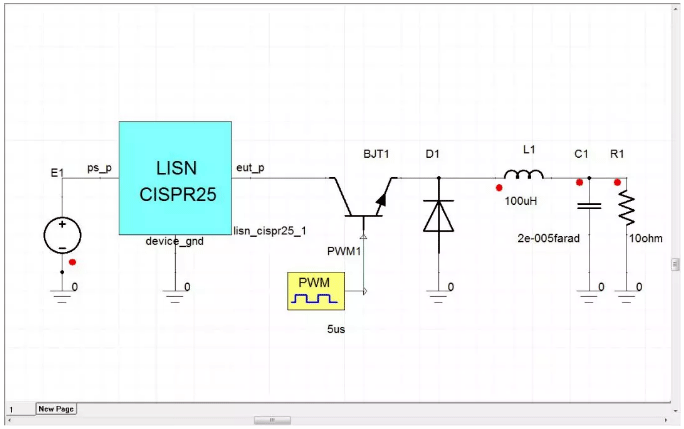
Figure 13 Buck Circuit Simulation Model
Figure 14 Voltage waveforms on each component
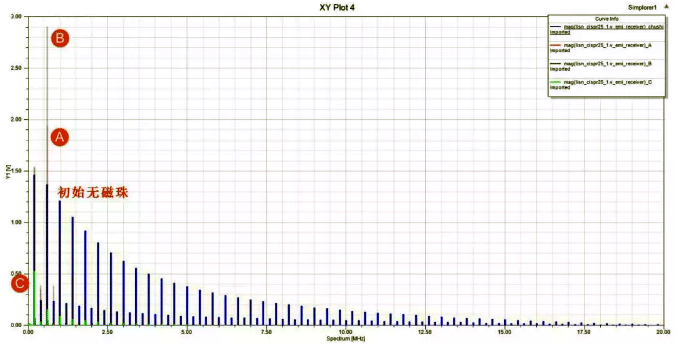
The following figure shows the conducted noise received by LISN, and it can be seen that the harmonics of the switching power supply itself are relatively rich. At a switching frequency of 200Khz, its harmonics extend up to 20MHz and are clearly visible. The duty cycle of the power switch tube is 50%. Theoretically, the amplitude of even harmonics at 50% duty cycle should be 0, but here it is a non-zero value. Why is this? This question is left for readers to ponder.
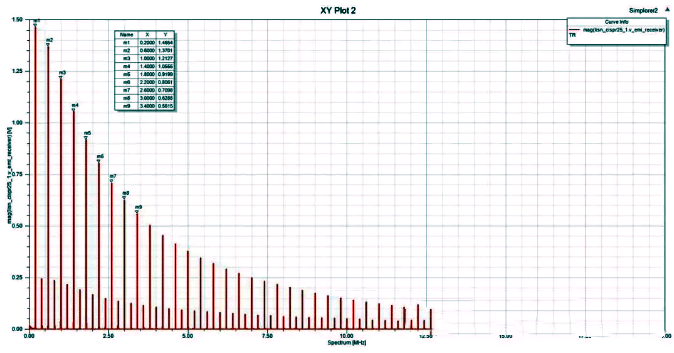
Figure 15 Conducted noise received by LISN end
Add the equivalent circuit of magnetic beads from the previous section to the power input terminal, as shown in the following figure, and observe the filtering effect of magnetic beads on switch noise in the circuit. Someone must be asking why we chose the magnetic beads with the highest impedance at high frequency (100MHz) to handle low-frequency noise. Readers with similar ideas should calm down and continue reading below. From the results, it can be seen that even high-frequency magnetic beads have a certain attenuation effect on power supply noise. As shown in the figure below, the voltage ripple on the inductor is significantly reduced, and the conducted noise received by LISN also decreases to a certain extent (note that this is a linear value, and this decrease can be ignored when converted to logarithmic value).
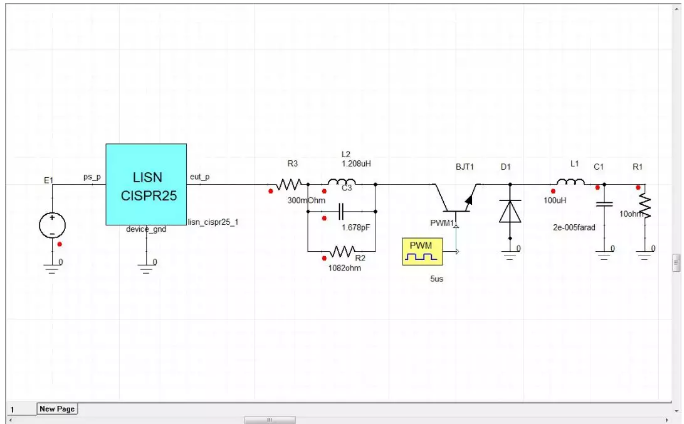
Figure 16 BUCK circuit after adding magnetic bead equivalent circuit
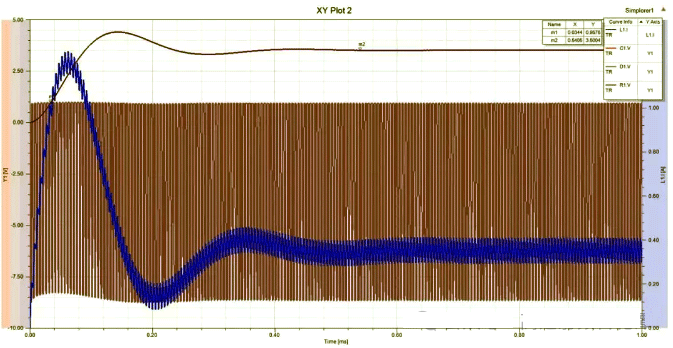
Figure 17 Voltage waveforms on each component after adding magnetic bead equivalent circuit
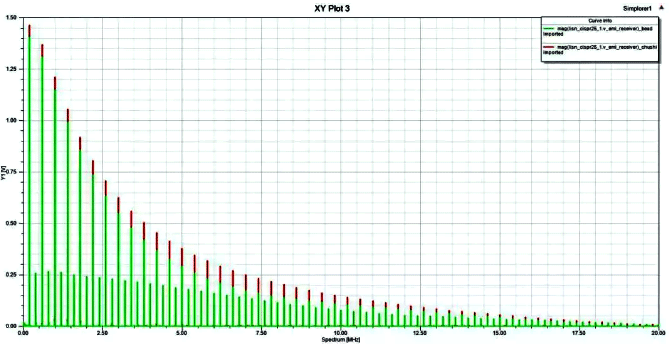
Figure 18 Comparison of Conducted Noise Received by LISN Before and After Adding Magnetic Beads
Some good people always use magnetic beads instead of inductors, placed at the power input end, and combined with capacitors to form a filtering circuit, as shown in the following figure. Adopting a similar approach can lead to a problem where the power input terminal experiences significant anti resonance in the low frequency range. As shown in the LISN results below, there is a significant decrease in noise after 1MHz. However, the noise amplitude before 0.6MHz is even higher than the power supply noise without filtering measures. It is disappointing that a certain number of engineers may choose to increase the capacitance value directly due to their lack of understanding of inductors, without realizing that the larger the capacitance value, the higher the low-frequency noise, and rectification is often confusing.
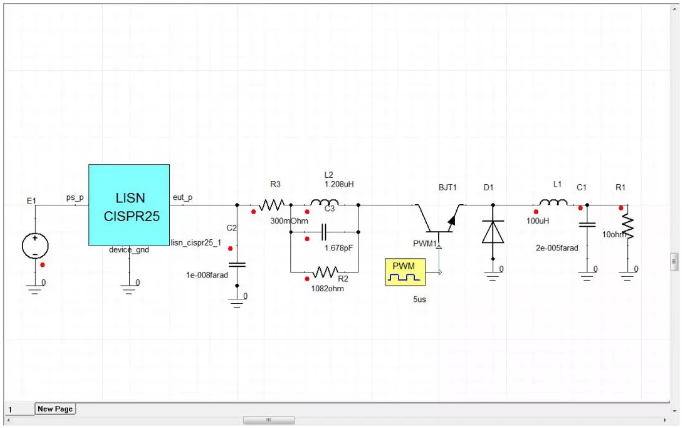
Figure 19 BUCK circuit with 10nF capacitor and magnetic beads (equivalent circuit replacement) added at the input terminal
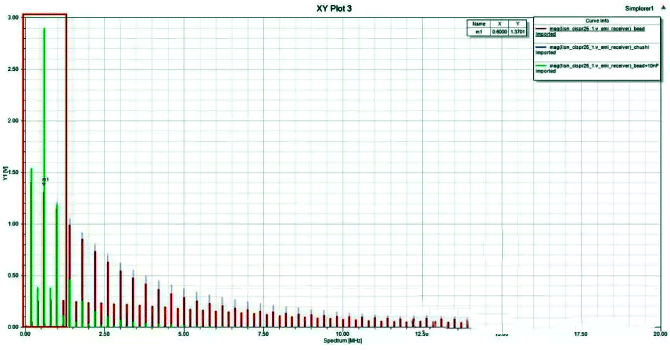
Figure 20 Conducted noise received by LISN in three different scenarios
When the resonant frequency of the low-pass filter network (composed of ferrite bead inductors and high-Q decoupling capacitors) is lower than the crossover frequency of the beads, a spike occurs. The filtering result is underdamped. The following figure shows the relationship curve between impedance and frequency measured by TDK MPZ1608S101A (provided in the literature). Resistive components (related to the dissipation of interference energy) have little effect until they reach a range of approximately 20 MHz to 30 MHz. Below this frequency, ferrite magnetic beads still have extremely high Q values and are used as ideal inductors. The LC resonant frequency of a typical ferrite bead filter is generally in the range of 0.1MHz to 10MHz. For typical switching frequencies in the range of 300kHz to 5MHz, more damping is required to reduce the Q value of the filter.
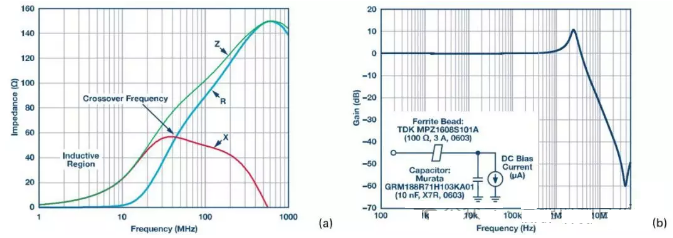
Figure 21 (a) A TDK MPZ1608S101A ZRX curve; Figure 21 (b) S21 response of ferrite beads and capacitor low-pass filter
An example of this effect is shown above; In the figure, the S21 frequency response of magnetic beads and the capacitance low-pass filter show peak effects. The ferrite beads used in this example are TDK MPZ1608S101A (100 Ω, 3A, 0603), and the decoupling capacitor used is Murata GRM188R71H103KA01 low ESR ceramic capacitor (10 nF, X7R, 0603). The load current is in the microampere level.
The undamped ferrite bead filter may exhibit peaks ranging from about 10dB to about 15dB, depending on the Q value of the filter circuit. In Figure 4b, the peak appears at around 2.5MHz with a gain of up to 10dB.
In addition, the signal gain is visible in the range of 1MHz to 3.5MHz. If the peak occurs within the operating frequency range of the switching regulator, there may be a problem. It will amplify interference switch artifacts, seriously affecting the performance of sensitive loads such as phase-locked loops (PLL), voltage controlled oscillators (VCO), and high-resolution analog-to-digital converters (ADC). The results shown in Figure 4b indicate the use of extremely light loads (microampere level), but this is a practical application for circuit parts that only require a few microamperes to 1mA load current or for parts that are turned off in certain operating modes to save power consumption. This potential spike generates additional noise in the system, which may lead to adverse crosstalk.

04
Methods for adjusting the damping of filtering systems
This section introduces several methods of adjusting damping that can be used to reduce resonance spike levels. Jefferson Eco proposed three methods in his article:
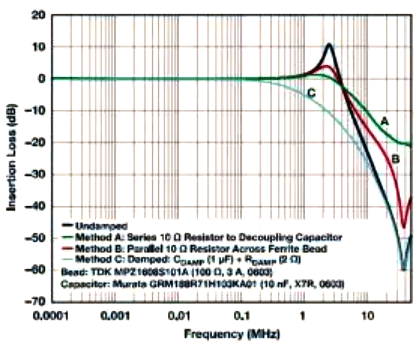
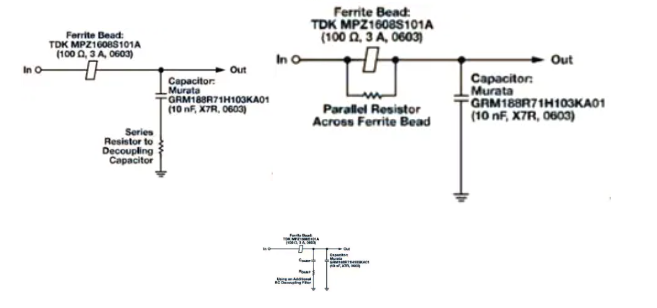
Frequency response of different damping methods in the figure
Method A involves adding a series resistor to the decoupling capacitor path, which can suppress system resonance but reduce the effectiveness of high-frequency bypass. Method B is to add a small parallel resistor at both ends of the ferrite bead, which will also suppress system resonance. However, the attenuation characteristics of the filter will decrease at high frequencies. The following figure shows the impedance frequency relationship curve of MPZ1608S101A with and without a 10 Ω parallel resistor. The light green dashed line represents the total impedance of the magnetic beads using a 10 Ω parallel resistor. The impedance and resistance combination of magnetic beads have significantly decreased and are mainly determined by a 10 Ω resistance. However, the 3.8MHz crossover frequency when using a 10 Ω parallel resistor is much lower than the crossover frequency of the magnetic beads themselves at 40.3MHz. Magnetic beads exhibit resistance in a much lower frequency range, which can reduce Q values and improve damping performance.
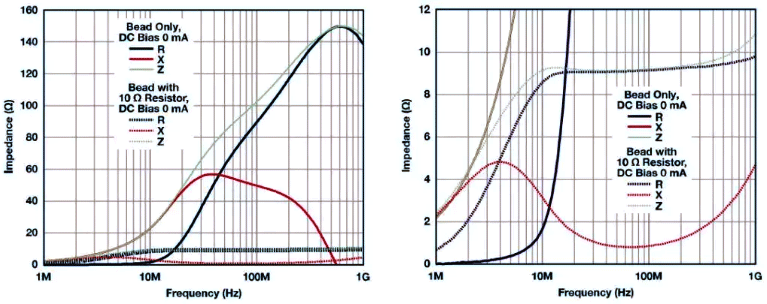
Figure MPZ1608S101A ZRX curve/MPZ1608S10101A ZRX curve
When applying the methods described in the literature to the switching power supply, it was found that the first two methods did not reduce the noise amplitude of 0.6MHz, while the third method effectively reduced all high-frequency harmonic noise.
The effect of applying three methods in the section switching power supply
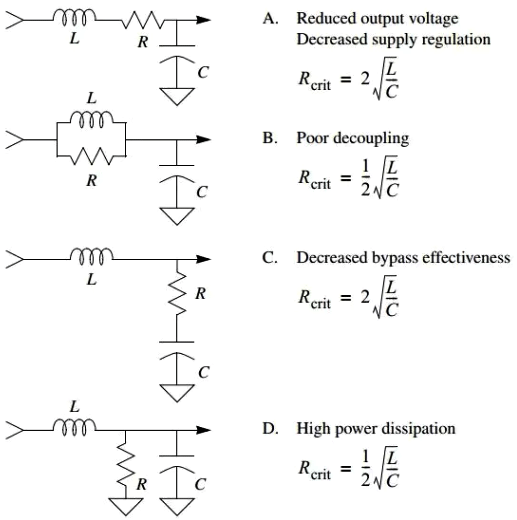
Compared to Jefferson Eco, Ken Kundert not only detailed how to handle underdamping in his article, but also provided calculation methods for each situation.
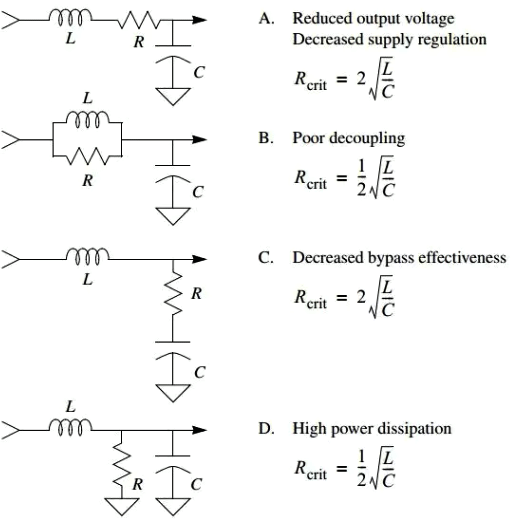
Several methods for decoupling graph damping networks and the required resistance value for critical damping
From the four methods provided by the author in the above figure, it is not difficult to see that they all have certain defects, to some extent sacrificing filtering insertion loss or signal power supply energy. To this end, the author added a damping adjustment method that satisfies both RCL parallel and series connections. As shown in the figure below, it can be seen that this method is identical to the method described by Jefferson Eco. The difference is that Ken Kundert further gives the relationship between 𝑅 𝑑 𝑎 𝑚 𝑝, 𝐶 𝑑 𝑎 𝑝, 𝐶 𝑏 𝑦, namely
The preferred method for providing damping in decoupling networks is shown in the figure
Due to the existence of many distributed parameters in actual circuits that we cannot accurately measure, the above methods are not always effective, and most engineers are not willing to try them. Here, Changhui Instrument proposes a simple and crude method, which is to filter out similar problems encountered in low-frequency switching frequency by increasing inductance. The sensitivity value should not be less than 50uH, of course, the setting of this target parameter is not fixed. The following figure shows the result of adding an inductor on the basis of magnetic beads, with the inductance value increasing from 10uH to 50uH. It can be seen that after increasing to 50uH, the noise amplitude of all harmonic components is lower than that without the initial filtering circuit.
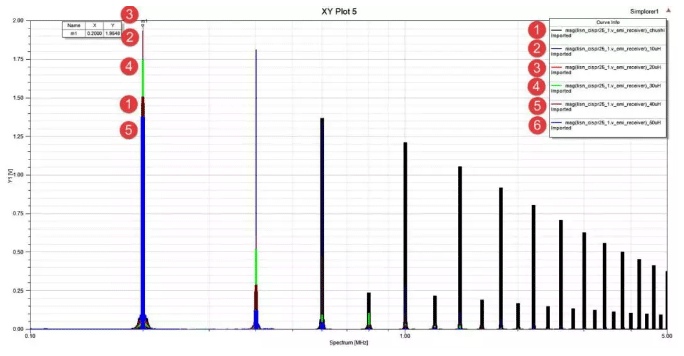
Adding inductance to the circuit to adjust damping
Because a 50% duty cycle is a special case, when the load is reduced from the initial 10 Ω to 2 Ω (simulating a fully loaded circuit), the duty cycle is approximately 64%. At this point, even harmonics are fully reflected, and increasing inductance is still applicable under full load conditions. However, the methods mentioned in the literature above still encounter situations where the low frequency exceeds the initial value.
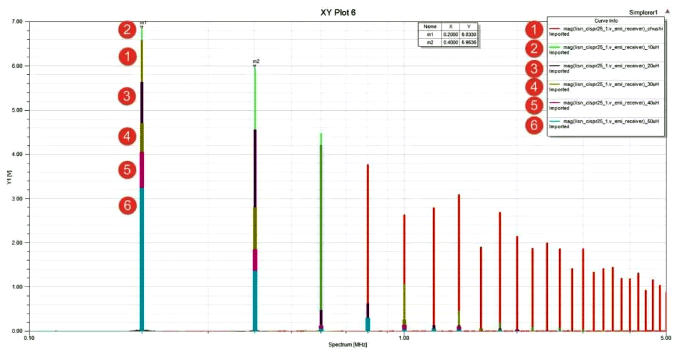
Figure The effect of adjusting the sensing value is still the same after the power load is increased
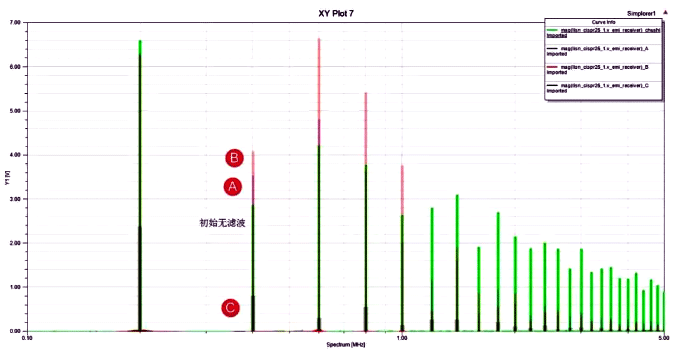
The conducted noise measured under heavy load using the three methods mentioned in the literature is shown in the figure
05
The influence of magnetic beads under DC bias
Choosing the correct ferrite magnetic beads for power applications not only requires consideration of the filter bandwidth, but also the impedance characteristics of the beads relative to the DC bias current. In most cases, manufacturers only specify the impedance of magnetic beads at 100MHz and publish the frequency response curve data manual at zero DC bias current. However, when using ferrite magnetic beads as a power filter, the load current through the beads is never zero, and as the DC bias current increases from zero, these parameters also change rapidly. As the DC bias current increases, the magnetic core material begins to saturate, resulting in a significant decrease in the inductance of ferrite beads. The saturation of inductance varies depending on the material used for the component magnetic core. The following figure shows the typical DC bias dependence of two ferrite magnetic beads. When the rated current is 50%, the inductance can decrease by up to 90%.
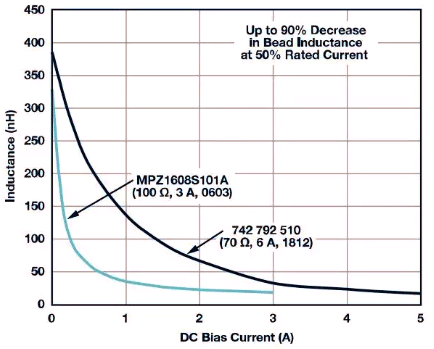
The influence of DC bias on magnetic bead inductance and its curve relative to DC bias current
The image uses TDKMPZ1608S10101A magnetic beads
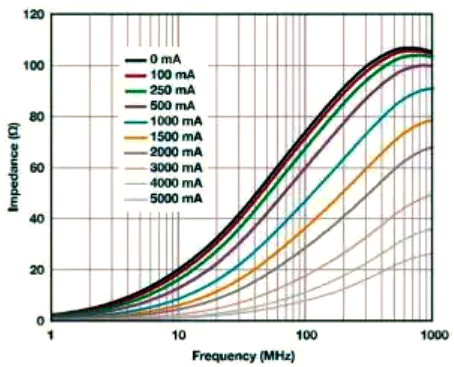
Figure 30c uses Wurth Elektronik 742 792 510 magnetic beads
If efficient filtering of power noise is required, according to design principles, ferrite beads should be used at approximately 20% of the rated DC current. As shown in these two examples, at a rated current of 20%, the inductance decreases to about 30% (6A magnetic beads) and about 15% (3A magnetic beads). The rated current of ferrite magnetic beads is the maximum current that the device can withstand under specified heating conditions, and is not the actual operating point for filtering purposes.
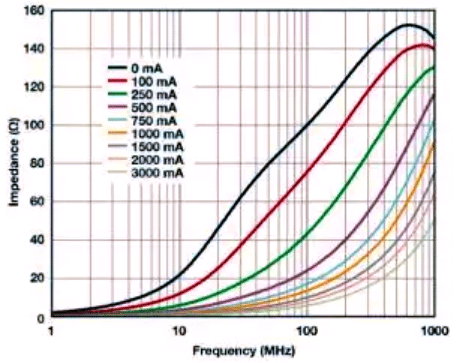
In addition, the effect of DC bias current can be observed by reducing the impedance value within the frequency range, thereby reducing the effectiveness of ferrite beads and their ability to eliminate EMI. Figures 30B and 30B show how the impedance of ferrite beads changes with the variation of DC bias current. By applying only 50% of the rated current, the effective impedance at 100MHz will significantly decrease from 100 Ω to 10 Ω (TDKMPZ1608S101A, 100 Ω, A, 0603), and from 70 Ω to 15 Ω (W ü rth Elektronik 742 792 510, 70 Ω, 6 A, 1812).